[CS] 다익스트라 알고리즘 (데이크스트라 알고리즘)

서론

오늘은 최단거리 알고리즘의 대명사 다익스트라 알고리즘에 대해서 알아보도록 하자. 지루하고 현학적인 이론을 설명하기에 앞서 EBS에서 누구나 다익스트라 알고리즘의 원리에 대해 아주 쉽게 시청각 자료를 곁들여서 설명을 해주었다(영상의 40초부터). 따라서 영상을 먼저 보고 온다면 이해해 큰 도움이 될 것이다.

다익스트라를 아주 쉽게 설명해준 EBS의 은혜

다익스트라 알고리즘(Dijkstra algorithm)이란?

다익스트라 알고리즘은 그래프에서 한 노드에서 모든 노드까지의 최단거리를 구하는 알고리즘이다. 영상을 보면 알다시피 Min distance table(MDT)로 불리는 최단거리배열을 갱신하며 최단거리를 구한다. 다익스트라의 핵심은 노드간의 탐색을 할때 현재 도달할 수 있는 간선의 비용중 가장 비용이 낮은 노드을 선택하여 탐색을 한다면 해당 노드로의 최단거리가 "확정"된다는 가정에서 시작하기에(영상에서는 최단거리가 확정된 노드를 핑크색으로 표시를 한다), 다익스트라 알고리즘은 탐욕법(Greedy) 알고리즘에 속하며 시간 복잡도는 $ O(NlogN + ElogV) $이다.

우선순위 큐를 사용한 개선된 다익스트라 알고리즘

우선순위 큐를 사용한 개선된 다익스트라 알고리즘

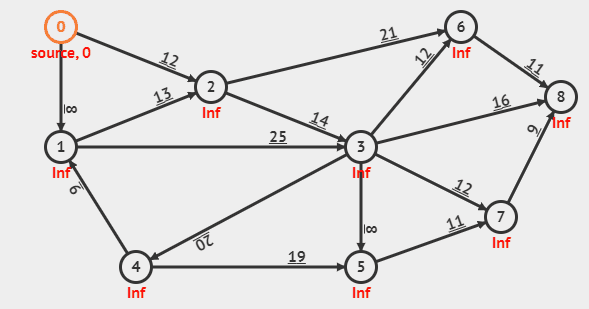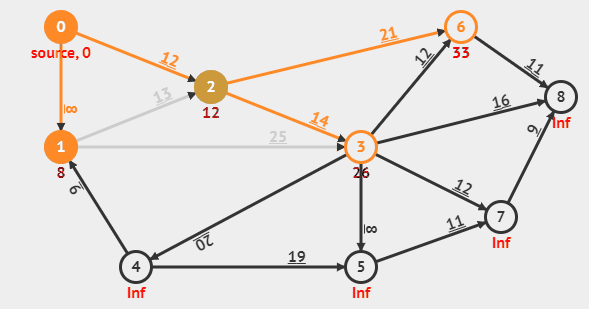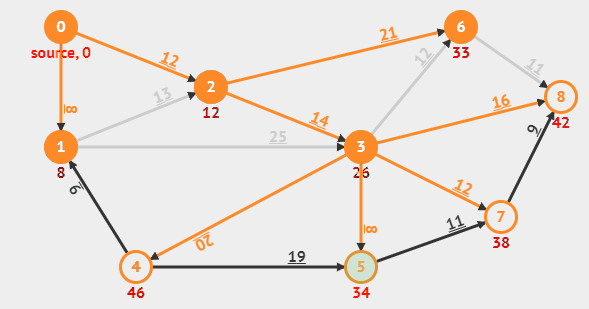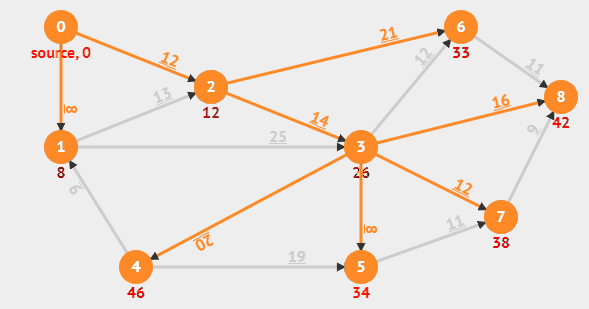
다익스트라의 기존 원리는 모든 노드$(O(N))$에 대해 선형 탐색으로 최소값을 추출하고$(O(N))$, 그에 따라 인접한 노드들의 최단거리를 갱신하는 과정$(O(E))$을 반복하는 방식이라서 전체 시간복잡도는 $O(N^2 + E)$이다. 하지만 이 방식은 노드 수가 많아질수록 비효율적이기 때문에, 이를 개선하기 위해 우선순위 큐를 사용한 방법이 등장했고, 우리가 일반적으로 말하는 다익스트라 알고리즘은 바로 이 우선순위 큐 기반의 개선된 버전이다. 개선된 다익스트라 알고리즘에서는 모든 노드$(O(N))$에 대해 우선순위 큐에서 최소값을 추출하는 데 $O(log⁡N)$, 그리고 최단거리 갱신 시 우선순위 큐에 값을 삽입하는 과정이 $O(log⁡N)$이라 전체적으로는 $O(Nlog⁡N+Elog⁡N)$이 소모된다.

 

 기존 알고리즘에서는 방문 여부 배열을 선형 탐색하면서 아직 방문하지 않은 노드 중 최단 거리인 노드를 찾아내는 과정이 $O(N)$이었다. 이 부분이 개선된 알고리즘에서는 우선순위 큐를 통해 $O(log⁡N)$으로 줄어든 것이다. 대신 기존에는 방문 여부 배열에 값을 단순히 삽입하는 비용이 $O(1)$이었는데, 우선순위 큐를 사용하게 되면서 이 삽입 비용이 $O(log⁡N)$으로 올라가긴 한다.

음수 간선

앞서 설명한바와 같이 다익스트라 알고리즘은 탐욕법을 기반으로 하기에 특정 노드로의 최단거리를 "확정" 하여 한번 확정된 노드는 두번다시 방문하지않는 것을 원칙으로 한다. 따라서 아래와 같이 그래프에 음수 간선이 존재할 경우 C를 이미 방문하였기 때문에 A->C에 대한 최단경로는 4가 되어버린다.

A -> C 최단경로

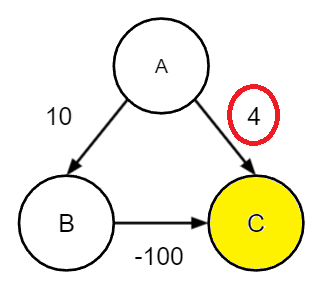
다익스트라 알고리즘은 무조건 음수 간선에 대한 처리를 못하는 것인가?

다익스트라 알고리즘에 대한 설명을 보면, 모든 간선의 가중치가 양수일 때 사용하는 것이 권장된다고 나와 있다. 그런데 이 알고리즘을 조금 변형해서 이미 방문한 노드도 다시 방문할 수 있도록 한다면, 음수 간선이 포함된 경우도 어느 정도 처리가 가능해진다. 하지만 이 경우, 알고리즘의 특성이 완전히 바뀌게 된다. 기존에는 한 번 방문한 노드는 다시 방문하지 않음으로써 그리디하게 진행됐는데, 중복 방문을 허용하게 되면 이는 사실상 백트래킹으로 바뀌게 된다.
이렇게 되면 결국 모든 간선을 전부 탐색해야 하기 때문에, 시간 복잡도도 증가하게 되는데, 이때의 시간 복잡도는$O(ElogE+ElogE)$, 즉$O(ElogE)$ 수준으로 늘어난다. 게다가 중복 방문이 허용된다는 특성 때문에, 만약 음수 간선들로 이루어진 사이클이 존재하게 되면, 알고리즘은 그 사이클 안에서 계속 돌게 되고, 루프에 갇혀버리게 된다. 그렇게 되면 결국 해를 도출해낼 수 없게 되는 것이다.
그래서 어떤 문제가 주어졌을 때, 만약 그 문제에 음수 간선이 존재할 수 있다면, 그리고 거기에서 음수 사이클이 없다는 조건이 명시되어 있지 않다면, 다익스트라 알고리즘을 사용하는 건 지양해야 한다. 이런 경우에는 벨만-포드(Bellman-Ford)처럼 음수 간선과 사이클까지 고려할 수 있는 알고리즘을 사용하는 것이 더 적합하다.

구현(C++)

다익스트라 알고리즘의 전개는 다음과 같다:

https://namu.wiki/w/%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

#include <bits/stdc++.h>
using namespace std;

int main()
{
	cin.tie(0)->sync_with_stdio(0);

	int n, m; cin >> n >> m;
	vector<vector<pair<int, int>>> graph(n); // { {cost, edge} }

	for (int i = 0; i < m; i++)
	{
		int a, b, c; cin >> a >> b >> c;

		graph[a].push_back({ c, b });
		graph[b].push_back({ c, a });
	}

	vector<int> mdt(n, INT_MAX); // 최단거리테이블 (Min distance table)
	vector<bool> confirmed(n, false);

	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // Cost를 기준으로한 Min Heap

	mdt[0] = 0;
	// 0번째 노드 삽입
	pq.push({ 0, 0 });

	while (!pq.empty())
	{
		auto [cost, node] = pq.top();
		pq.pop();

		if (node == n - 1) break;
        if (confirmed[node]) continue;
		confirmed[node] = true; // 노드 확정

		for (auto [nextCost, nextNode] : graph[node])
		{
			if (confirmed[nextNode]) continue; // 확정된 노드인지 Check
			if (mdt[nextNode] > mdt[node] + nextCost)
			{
				mdt[nextNode] = mdt[node] + nextCost;
				pq.push({ mdt[nextNode], nextNode });
			}
		}
	}
	cout << mdt[n - 1];
}